Abel, Thiên Tài và Bạc Mệnh
Bài viết này đuợc trích ra trong chương “Những Vương Công Trong Toán Học” của cuốn sách Vui Đời Toán Học của giáo sư Nguyển Xuân Vinh. Mỗi bài viết là một câu chuyện lư thú được tác giả kể với ng̣i bút bác học của ḿnh. Điều đặc biệt ở đây là dù kể chuyện xẩy ra ở nước người, ông cũng đưa vào chút h́nh ảnh của quê hương và chen thêm kỷ niệm và tâm sự riêng của ḿnh.
Tháng 5 năm Nhâm Tuất (1802), vua Gia Long lên ngôi tôn, sáng lập triều đại quân chủ cuối cùng của Việt Nam. Tuy những vị vua của triều Nguyễn đều là những vị thông minh, học thức, nhưng các quan triều đ́nh lại là những người thủ cựu, mỗi khi có sĩ phu thức thời làm biểu xin canh tân đất nước, lúc nhà vua đưa ra triều đ́nh nghị sự th́ lại được nghe những lời tâu bầy là ư kiến không hợp thời thế. Trong suốt thế kỷ thứ 18 và 19, trên mọi phương diện kinh doanh, kỹ nghệ, ngoại giao, … nước ta như đứng dừng lại. Chỉ đôi khi gặp người thao lược như doanh điền sứ Nguyễn Công Trứ giúp dân khai khẩn thêm đất mầu ở những miền Kim Sơn, Tiền Hải, chấn hưng canh nông, hay được những văn thi hào như Nguyễn Du, Đoàn Thị Điểm, Nguyễn Đ́nh Chiểu sáng tác và lưu lại cho đời sau những thi phẩm tuyệt tác là c̣n được đôi chút gọi là mở mang khai hóa mà thôi.
Cũng vào năm ấy, ở cách nửa địa cầu bên trời Tây đă bắt đầu một thế kỷ sáng tác chói lọi nhất của lịch sử toán học. Nếu một nhà chiêm tinh nào, ban đêm nh́n giải thiên hà mà thấy rằng có nhiều v́ sao sáng, mỗi v́ sao ứng vào một thiên tài toán học đang ở trần thế, v́ sao sáng nhất phải chiếu vào toán gia lỗi lạc nhất là Niels Henrik Abel. Tuy Abel chỉ sống dưới trần gian một thời gian ngắn ngủi là gần 27 năm mà công nghiệp của nhà thiên tài này đă làm cho một nhà toán học lỗi lạc khác là Charles Hermite (1822-1901) phải nói rằng: “Abel đă để lại công tŕnh làm cho các toán gia hậu thế bận rộn vào khoảng 500 năm mới khai thác hết”.
Nhà thiên tài toán học này không phải là người nước Pháp hay nước Đức là những nước chia ngôi bá chủ khoa học của thế kỷ 19. Ông sinh ngày 5 tháng Tám, năm 1802 ở một làng nhỏ bé tên là Findo của Na Uy, và là con thứ hai của vị mục sư trong làng. Bà mẹ ông là Anne Marie, là người có nhan sắc, và cũng thích ăn diện, làm đỏm đáng. Cũng v́ vậy mà gia đ́nh ông mục sư luôn luôn túng thiếu, thêm nỗi nheo nhóc v́ đông con. Trước Abel có một người chị, và sau đó chàng trai trẻ khi lớn lên phải chăm lo cả cho 5 đứa em sinh sau ḿnh.
Ngay từ khi c̣n học ở bậc tiểu học, Abel đă bộc lộ chàng có một thiên tài toán học. Như ở các xă hội Âu châu thời đó, các thầy giáo rất nghiêm khắc với các học tṛ. Một cậu bạn cùng lớp với Abel đă bị ông giáo ác nghiệt cho đánh đ̣n nặng nề đến nỗi bị chết v́ những vết thương quá nặng và một ông thầy khác thiên về toán pháp đuợc chuyển đến thay cho ông giáo hung thần của đám học tṛ. Vị thầy học mới tên là Bernt Michael Holmboe (1795-1850). Tuy không phải là một nhà toán học xuất sắc, nhưng chỉ trong ba tuần lễ sau khi nhận việc ông thầy đă thấy ngay là cậu học tṛ của ḿnh sau này sẽ làm cho nước Na Uy được thế giới toán học biết tới, và trong suốt cuộc đời của Abel, ông luôn luôn t́m cách giúp đỡ chàng, đôi khi phải tiêu vào cả số lương giáo học nhỏ nhoi của ḿnh. Na Uy lúc đó là một nước nghèo sau những lần chiến tranh với Anh Quốc và Thụy Điển, rồi lại bị những năm mất mùa làm kiêt quệ ngân sách quốc gia. V́ vậy lúc đầu Abel đă không được một học bổng trợ cấp nào của chính phủ.
Khởi đầu, với sự hướng dẫn của Holmboe, Abel, tuy lúc đó mới 16 tuổi, ngoài chương tŕnh học cùng với các bạn trong lớp, đă bắt đầu học thêm những công tŕnh toán học cận đại của các toán gia lừng danh như Newton ở Anh, Euler ở Thụy Sĩ và Nga, và Lagrange ở Pháp. Từ đó mà kiến thức Toán và phát minh lư thuyết mới của Abel nở ra lộng lẫy. Mấy năm sau có người hỏi chàng là làm cách nào mà vượt lên hàng đầu một cách nhanh chóng như vậy th́ Abel đă trả lời là: “Tôi học hỏi ở những vị thầy chứ không học ở các học tṛ của họ.” Trong khi nghiên cứu những lư thuyết viết ra bởi những bậc thầy đi trước, Abel t́m ra rằng ngay cả những bậc kỳ tài về toán học ở thế hệ trước như Léonard Euler (1707-1783) và Joseph-Louis Lagrange (1736-1813) đă có những chỗ chứng minh c̣n sơ hở. Trong cuộc đời ngắn ngủi của chàng, Abel cũng đă bỏ ra nhiều th́ giờ để hoàn chỉnh một số định lư toán học. Chàng đă lấp những chỗ c̣n để trống của những người đi trước. Bức tường thành toán học đă được xây dựng lên, nay không c̣n khe hở nào nữa.
Khi Abel vừa tṛn 18 tuổi th́ vị mục sư thân phụ của chàng mệnh một ở tuổi 48, để lại cho cậu con thứ nh́ gánh nặng phải chu toàn cho bà me, một người chị và năm đứa em. Chàng tuổi trẻ, có thiên tài toán học, lúc nào tính t́nh cũng lạc quan, nên dù thường xuyên sống trong thiếu thốn mà lúc nào cũng vui vẻ. Mộng của Abel là đạt được một số công tŕnh toán học xuất sắc, để rồi trong tương lai được mời làm giáo sư toán ở một trường đại học quốc gia. Trong khi chờ đợi, chàng kiếm một vài chỗ dậy học tư, kèm toán cho những trẻ, con nhà giàu có. Về môn dậy học, Abel đă là một thầy giáo tận tâm và kiên nhẫn. Thêm vào nữa là ở những trường công dạo đó ít có thầy giỏi, v́ số lương bổng cho giáo chức quá ít ỏi nên lúc nào Abel cũng được nhiều học sinh đến xin học tư để được chàng kèm về môn toán pháp. Cũng v́ làm việc lao lực quá độ mà sau này Abel lâm bệnh hiểm nghèo.
Một bài toán khó khăn mà tất cả các toán gia thời đại trước và đương thời không một ai t́m thấy lời giải là t́m nghiệm số cho phương tŕnh đại số bậc năm. Abel đă tự nguyện là sẽ giải bài toán này.
Đến đây ta hăy tạm dừng và trở về với đất nước Việt Nam, xét lại vấn đề học hành thời đó, và t́m hiểu chút ít về những phương tŕnh đại số qua một vài câu chuyện vui về toán học.
Ông trạng toán và những phương tŕnh đại số
Qua những khó khăn khi t́m việc của Abel, ta đă thấy ở những thế kỷ trước ở Âu châu, muốn thành một giáo sư, ngoài vốn học thức phải được sự tiến cử của đồng nghiệp. Ở nước ta, từ thế kỷ XI, triều đại nhà Lư bắt đầu dùng chế độ khoa cử rồi tuyển dụng quan lại trong số những người có bằng cấp. Dưới triều nhà Nguyễn vào thế kỷ 19 mà ta đang xét tới, thi cử có 3 kỳ, ở ba cấp bậc là những kỳ thi Hương, thi Hội và thi Đ́nh. Thi Hương cứ ba năm tổ chức một lần ở nhiều nơi. Thời đó ta có các trường thi từ Nam ra Bắc là ở An Giang, Gia Định, B́nh Định, Thừa Thiên, Nghệ An, Thanh Hoá, Nam Định và Hà Nội. Thi Hương gồm 4 kỳ gọi là nhất trường, nhị trường, tam trường và tứ trường; thí sinh trúng kỳ trước mới được vào kỳ sau. Trúng 4 kỳ là cử nhân, trúng 3 kỳ là tú tài. Số người đi thi ở mỗi nơi kể có hàng ngàn. Lúc lấy đỗ cử nhân c̣n vào khoảng 30 người và tú tài chừng 75 người.
Các vị quan ở trong triều được cử ra làm chánh chủ khảo các trường thi đều có biển đề bốn chữ “Phụng chỉ cầu hiền” là vâng lệnh vua ra t́m người tài giỏi đức độ. Qua năm sau có khoa thi Hội tại bộ Lễ ở kinh đô để những người có học vị cử nhân dự thí. Ai trúng cách th́ được vào sân đ́nh nhà vua thi một kỳ cuối cùng, gọi là thi Đ́nh. Những người thi Đ́nh trúng cách được học vị tiến sĩ, nhưng cũng có thứ bực phân biệt được xếp hạng vào ba cái bảng gọi là giáp. V́ vậy ta hay dùng từ khoa bảng hay khoa giáp để chỉ những người có bằng cấp. Ba người giỏi nhất được ghi tên trên bảng đầu gọi là đệ nhất giáp, và theo thứ tự được đề tên trước hay tên sau mà gọi là đệ nhất giáp-đệ nhất danh, đệ nhị danh, và đệ tam danh. Người đứng đầu gọi là Trạng Nguyên, người thứ hai là Bảng Nhăn và người thứ ba là Thám Hoa. Những người được ghi tên vào bảng thứ hai, gọi là đệ nhị giáp, là các ông tiến sĩ xuất thân. Những người xuất sắc khác, cũng trúng cách, được ghi tên vào bảng thứ ba, gọi là đệ tam giáp. Học vị của họ là đồng tiến sĩ xuất thân. Trung b́nh th́ số lượng tiến sĩ mỗi kỳ vào khoảng hơn hai mươi người. Mỗi kỳ c̣n có vài người, học lực cũng xứng đáng là tiến sĩ, nhưng văn bài đôi khi có điểm thiếu sót, được ghi tên trên một bảng phụ và được nhận học vị phó bảng.
Những người có học vị từ cử nhân trở lên, dần dà được bổ nhiệm các chức vụ hành chánh ở các châu, huyện hay phủ và dần dần thăng quan tiến chức. Những người theo học chánh, được gọi là học quan, có chức vụ là huấn đạo để coi việc học ở châu, huyện nhỏ, chức vụ giáo thụ coi việc học ở phủ hay huyện hay cao hơn là chức đốc học để coi sóc việc học ở cấp tỉnh. Ở triều Nguyễn, quan chức văn vơ chia làm chín phẩm, mỗi phẩm lại có chánh và ṭng, th́ đốc học ở hàng chánh ngũ phẩm, giáo thụ ở hàng chánh thất phẩm và huấn đạo ở hàng chánh bát phẩm.
Ở triều Nguyễn, v́ sợ những người có học vị cao mà sinh ra kiêu căng, tự phụ, nên có lệ là không phong học vị Trạng Nguyên. Tuy vậy, người dân, tự cổ xưa, vẫn qúy trọng những người có thực tài, và dùng chữ trạng để gọi những người có tài đặc biệt, xuất sắc hơn người, như ở làng Mộ Trạch ở Hải Dương có ông Vơ Phong được gọi là trạng vật v́ đă đánh ngă được lực sĩ của vua Lê Thánh Tông, và Vơ Huyên được gọi là trạng cờ v́ vô địch về môn này. Về thời đại vua Lê Cảnh Hưng và chúa Trịnh, có ông Nguyễn Quỳnh (1677-1748) chỉ đỗ cử nhân, nhưng v́ có tài biện bác nên dân chúng gọi là Trạng Quỳnh và đặt ra nhiều truyền thuyết về ông.
Bài viết này, hướng về những ông hoàng trong toán học mà thi cử ở Việt Nam qua các triều đại chỉ khảo sát về kinh nghĩa, chiếu, chế, biểu và thơ phú cùng văn sách, chọn những người giỏi thảo luận văn chương, kinh sử, văn thơ viết lưu loát. Chỉ trong triều đại ngắn ngủi ở nhà Hồ (1400-1407), trong những khoa thi Hương mới đặt thêm một kỳ thi toán pháp mà thôi. Tuy vậy trong những ông trạng Việt Nam cũng đặc biệt có ông Lương Thế Vinh, sinh năm 1441 tại Cao Hương, huyện Thiên Bản nay đổi là Vụ Bản, tỉnh Nam Định, đậu trạng nguyên khoa Quí Mùi, năm Quang Thuận thứ tư, đời vua Lê Thánh Tông (1463), là người có tài văn chương mà cũng tinh thông khoa học và toán pháp.
Nhiều người trong chúng ta đă được đọc trong sách quốc văn chuyện ông Lương Thế Vinh chơi cầu với trẻ mục đồng, để quả bưởi làm bóng đá lọt xuống một hố xâu đă lấy nước đổ vào để làm nổi quả bưởi lên và lấy ra được, tức là ông đă áp dụng nguyên lư tỷ trọng của Archimedes. Nhưng ít ai biết được rằng, Ở thế kỷ XV ông đă soạn ra cuốn “Đại Thành Toán Pháp” để phổ biến kiến thức toán học thời đó áp dụng vào đời sống hàng ngày. Trong cuốn sách, nếu so sánh với lư thuyết đương thời th́ cũng có những điều ông tự biên chế mà ra. Nói chung th́ trong sách có dậy những phương pháp phân chia ruộng đất, tính diện tích các h́nh, đo các chiều dài theo phương pháp đồng dạng. Vào thời ấy phải những người có năng khiếu toán học mới thấu triệt những quy tắc ấy.
Vào khoảng hơn một trăm năm, trước thời đại của Lương Thế Vinh, dưới đời nhà Trần cũng có một ông Trạng có óc thông minh tuyệt vời, giỏi văn chương lại có tài biện bác là Mạc Đĩnh Chi. Ông thi đậu Trạng nguyên năm 1304, thời vua Trần Anh Tông. Lúc vào điện nhận áo mũ, vua thấy ông người xấu xí nhỏ bé có ư không muốn dùng. Ông về nhà làm bài phú “Ngọc Tỉnh Liên” ví ḿnh như bông hoa sen dưới giếng ngọc. Có người dâng lên vua đọc. Trần Anh Tông vời ông ra làm quan, sau này sang sứ nhà Nguyên bên Tàu, gây được sự kính nể của người ngoại bang. Truyền tụng lại đời sau, có sự việc là vua nhà Nguyên thấy ông đối đáp lưu loát, thảo văn chiếu phong phú, mạch lạc, có tài vượt bực nên phong cho ông là Lưỡng Quốc Trạng Nguyên.
Một truyện c̣n được chép lại trong cuốn “Nam Hải Dị Nhân” của học giả Phan Kế Bính là một lần đi sứ sang Trung Quốc, dự tang lễ một bà hoàng phi được vua Tàu sủng ái, ông được mời đọc bản văn tế, khi mở ra chỉ có bốn chữ Nhất , ngụ ư là cái ǵ cũng tuyệt vời. Ông đọc ra ngay bài văn và sau này chép lại rằng:
Thanh thiên Nhất đoá vân,
Hồng lô Nhất điểm tuyết,
Thượng uyển Nhất chi hoa,
Giao tŕ Nhất phiến nguyệt.
Y! Vân tán, Tuyết tiêu, Hoa tàn, Nguyệt khuyết!
Bài văn tế có bốn chữ nhất, là số Một dịch là:
Trời xanh Một đám mây,
Ḷ hồng Một giọt tuyết,
Thượng uyển Một cành hoa,
Giao tŕ, trăng Một mảnh.
Than ôi! Mây rời, tuyết tan, hoa tàn, trăng khuyết!
Nhân dịp kể chuyện tài năng toán học ở nước người vào thế kỷ 19, mà lùi lại ba, bốn trăm năm để nói về những thiên tài ở nước ḿnh là tôi muốn đưa ra nhận xét rằng Mạc Đĩnh Chi, Lương Thế Vinh và nhiều nhân tài khác ở nước ḿnh như Lê Qúy Đôn, Ngô Thời Nhiệm, Đào Duy Từ và ở thời cận đại như Cao Thắng, nếu chương tŕnh học hành được tổ chức khác, thay v́ học làu kinh sử rồi tới thụ huấn những vị đại khoa để nghe giảng văn, b́nh luận, mà được đem trí thông minh ra t́m hiểu những định luật thiên nhiên, dùng luận lư đạt thành toán học th́ đất nước Việt Nam cũng sản xuất ra những người sánh được với Descartes, Pascal, hay Newton và Leibniz là những người đă đặt những viên đá nền tảng để xây dựng lâu đài toán học thế giới.
Nhân câu chuyện những phương tŕnh đại số, mà như ta đă kể ở trên, trải qua ba trăm năm, không một toán gia nào t́m được phương pháp giải phương tŕnh bậc năm, phải đợi đến thời Abel, vào năm 1821, khi vào khoảng 19 tuổi, ông đă chứng minh được rằng phương tŕnh không có lời giải bằng đại số, ta thử t́m hiểu chút ít về sự ích lợi của đại số học, và đặc biệt lấy một thí dụ vui về phương tŕnh bậc nhất.
Ta tưởng tượng ra rằng có một sứ thần Việt Nam sang Tàu triều kiến thiên triều, và vua ta đă cử một ông Trạng, tạm gọi là Trạng Toán v́ có tài đă học qua “Đại thành toán pháp” của Lương Thế Vinh, lại nhanh trí biện bác như Mạc Đĩnh Chi. Vào một buổi vua ban ngự yến, có nhiều sứ giả của các nước Tây phương, và các nước biên phương như Ngoại Mông, Cao Ly, Tây Vực, …., Vua muốn thử tài nên bày ra những mục thi văn thơ, toán đố. Về những môn khởi đầu th́ ông Trạng nhà ta hơn người vượt bực, v́ đó là lối quen tập làm văn bài từ thuở nhỏ theo lối học hành khoa cử của ḿnh. Cuối cùng tới mục toán đố, nhà vua cho một vị quan chuyển tới từng sứ thần đầu bài:
“Trong vườn thượng uyển có hai loại chim và thú tổng cộng có 36 con. Loại thú gồm những con, mỗi con có 4 chân. Loại chim như công, phượng, trĩ, … mỗi con có 2 chân. Thị vệ đă đếm cẩn thận thấy tổng cộng cả cầm lẫn thú có 100 chân. Vậy có bao nhiêu con chim và bao nhiêu con thú?”
Trạng Việt Nam nhớ ngay đây là bài toán dân gian ở nước ḿnh, nôm na là: “Vừa gà vừa chó 36 con. Trói lại cho tṛn, 100 chân chẵn. Vậy gà mấy con, chó mấy con?” Không hiểu bằng cách nào bài này lại truyền sang Bắc Kinh. Sau khi nhận đầu bài, sứ thần Tây phương loay hoay viết bài giải, c̣n sứ thần các nước chịu ảnh hưởng khoa toán pháp của Trung Hoa th́ dùng bàn tính, gẩy lách cách, trừ đi cộng lại theo lối tính nhẩm. Trạng Toán biết rằng, sớm hay muộn th́ sứ thần các nước cũng t́m ra lời giải, và muốn cho lời đáp của ḿnh được công bố trước nhất, Trạng ta viết đại hai gạch chéo, đọc theo kiểu bây giờ là chữ X , và tŕnh ngay lên nhà vua. Đó là Trạng đă dùng phương pháp tượng trưng lời văn giải đáp như khi xưa Mạc Đĩnh Chi chỉ có một chữ nhất mà diễn đạt được một bài thơ đượm ư t́nh một cách tuyệt vời.
Sau chừng nửa giờ, trống lầu điểm kết thúc, trừ một vài sứ thần các nước man di v́ không hiểu thấu triệt đầu bài nên không giải nổi, c̣n các ông trạng đi sứ của các nước khác đều có lời giải đáp đúng là 14 con thú và 22 con chim. Cộng lại tổng cộng là 14+22 = 36 con. Số chân th́ con thú có 14 x 4 = 56 chân và số chim có 22 x 2 = 44 chân. Cộng lại cũng đúng là 56 + 44 = 100 chân.
Sau khi tuyên bố kết quả, Vua Tàu khen ngợi những người trúng cách và phán rằng nếu hai gạch chéo thành chữ X là lối chữ viết chỉ đúng số thú hay số chim, th́ Trạng Việt Nam đă là người giỏi nhất ở đủ mọi môn, xứng đáng là Lưỡng Quốc Trạng Nguyên, Văn Toán song toàn. Lúc đó trạng Việt Nam mới dùng phương pháp biện bạch của Mạc Đĩnh Chi và lư luận toán pháp của Lương Thế Vinh mà tâu vua:
- Chữ X của hạ thần có thể dừng để chỉ số thú, hay dùng để chỉ số chim cũng được. Xin hoàng thượng ban kim lệnh.
Nhà vua ngần ngừ rồi nghĩ đến loài gấu Panda mới có:
- Được, cho đấy là số thú.
- Tâu bệ hạ, v́ tổng số cầm thú là 36 con nên loài chim có (36-x) con.
Vua gật đầu, chịu là phải, và hỏi:
- Vậy số chân th́ sao?
- Tâu bệ hạ, v́ có x con thú, nên số chân của thú là 4x, và v́ có (36-x) con chim nên nhân với 2, có số chân của các loài chim là 2(36-x).
Vua chịu Trạng Toán là lư luận giỏi. Nhưng hoàng thượng hỏi thêm:
- Nếu không đúng là 100 chân th́ sao?
Trạng trả lời:
- Tâu bệ hạ, phương pháp đại số (Trạng nghĩ đến sự việc thay đại một con số mà nói vậy) của hạ thần bao giờ cũng chính xác. Đem cộng vào chắc chắn là đủ số 100 chân. Xin tŕnh hoàng thượng như sau:
Cộng lại là
4x + 2(36-x) = 100
Nhân ra
4x + 72 – 2x = 100
Làm giản dị
2x = 28
Nếu 2 lần số thú là 28 con, th́ số thú là 14 con. C̣n lại số chim tất nhiên là 22 con.
Bài tính trên là một thí dụ toán đại số đưa đến một phương tŕnh bậc nhất. Số x gọi là ẩn số, ta muốn t́m ra trị số. Khi theo đầu đề mà viết ra bài tính, bao giờ ta cũng có một phương tŕnh dưới dạng
ax + b = 0
mà a và b là hai hệ số biết rồi. Chẳng hạn như phương tŕnh của bài toán cầm và thú ở trên th́ a = 2 và b = -28. Lời giải của phương tŕnh bậc nhất viết theo dạng thu gọn ở trên là
x = -b/a.
Nhiều bài toán thông dụng hàng ngày, dùng toán đại số với x là ẩn số, đưa ta đến một phương tŕnh bậc nhất như ở trên và sẽ cho ta ngay lời giải. Vậy phương tŕnh bậc hai là thế nào, và lời giải khó khăn ra sao? Ta lại dùng câu chuyện ông Trạng Toán để t́m hiểu đề toán này.
Một hôm Trạng Việt Nam được vời vào chầu vua lúc đó đang đi suy nghĩ một ḿnh trong sân đ́nh. Trông thấy Trạng, nhà vua vẫy lại gần một chiếc bàn và chỉ vào một h́nh đă vẽ sẵn trên cát và bảo:
- Trạng lại dùng chữ x mà giải cho ta điều khó khăn này. Trẫm đă bảo quan thiên giám và thượng thư công bộ t́m cách giải mà chưa có kết quả.
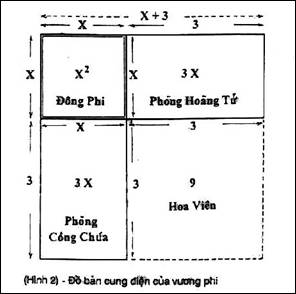
Trạng Toán nh́n trên đồ h́nh và theo lời giải thích của nhà vua, th́ vua muốn xây một Đông cung cho một bà hoàng phi rất được sủng ái. Bà vương phi này hạ sinh được một hoàng tử và một công chúa. Cung điện được xây theo h́nh thước thợ. Ở góc chính là một điện vuông vắn cho bà hoàng phi ở. Kéo dài về phía đông là cung pḥng cho hoàng tử, chiều ngang bằng kích thước cung pḥng cho bà hoàng phi, c̣n chiều dài về phía đông là đúng 3 sải. Vào thời bấy giờ mỗi sải dài chừng mười trượng. Từ cung pḥng của bà hoàng phi kéo dài về phía nam là cung pḥng của công chúa, kích thước cũng như cung pḥng của hoàng tử. Nh́n thoáng qua đồ h́nh, Trạng nói ngay:
- Tâu hoàng thượng, như vậy thần xin gọi x là kích thước vuông vắn cung pḥng của lệnh bà.
Vua gật đầu cho là có lư, v́ nay mới chỉ biết chiều dài của cung pḥng của hoàng tử và của công chúa là 3 sải, c̣n chiều rộng chưa biết là bao nhiêu, rơ ràng là ẩn số rồi c̣n ǵ nữa. Vả chăng, xưa nay quan trạng Việt Nam cái ǵ không biết cứ tạm gọi đại là x, rồi sẽ t́m hiểu sau. Trạng lại nói tiếp:
- Như theo lối tính diện tích th́ diện tích cung pḥng của lệnh bà là x2, của hoàng tử là 3x và của công chúa cũng là 3x.
Vua gật đầu khen phải và nói thêm:
- Nhưng cung điện xây cất cho vương phi không được to hơn là chính cung. Quan thượng thư công bộ đă cho biết là số đá hoa để lát pḥng từ Tây phương gửi sang triều cống dành cho việc này là đúng 16 sải vuông. Vậy Trạng tính làm sao cho đủ.
Được lệnh, Trạng ta viết ra phương tŕnh, cộng diện tích cả ba cung pḥng lại sao cho bằng 16 nghĩa là
x2 + 6x = 16
Phương tŕnh này gọi là phương tŕnh bậc hai v́ số mũ cao nhất của ẩn số là 2. Nói chung phương tŕnh bậc hai có dạng tổng quát là
a x2 + bx + c = 0
khi a, b, và c là những số cho biết, và x là ẩn số phải tính ra. Như phương t́nh của cung điện ở trên th́ ta có a = 1, b = 6 và c = - 16. Bài toán là làm thế nào chỉ dùng ba số a, b và c, làm một vài phép tính hữu hạn, nghĩa không phải tính lập lại hàng trăm lần, mà t́m ra trị số của x.
Toán gia người Ả Rập tên là Mohammed ibn Musa Al-Khowarizmi là người đầu tiên t́m ra công thức giải phương tŕnh bậc hai này và viết trong cuốn sách in ra năm 825. Cũng từ tên sách theo chữ Ả Rập là al-jabr, có nghĩa là thu gọn, mà trở thành tên algebra đặt cho môn đại số. Quan trạng, sứ thần Việt Nam, v́ không được học phương pháp tính toán của phương Tây, nên không biết công thức giải toán phương tŕnh bậc hai, nhưng nhờ h́nh vẽ mà Trạng ta t́m ra lối giải, cũng đúng như phép giải của Al-Khowarizmi.
Sau khi nh́n h́nh vẽ các cung pḥng, Trạng tâu với nhà vua:
- Tâu Hoàng thượng, nếu khoảng đất trống được bao hai phía bởi những cung pḥng của hoàng tử và công chúa được dùng làm vườn hoa th́ khu cung điện của vương phi thành một h́nh vuông vắn và có vẻ uy nghi, bề thế.
Nhà vua khen phải và bảo Trạng cộng thêm khu đất vuông, mỗi chiều 3 sải, tức là 9 sải vuông. Như thế thành
x2 + 6x + 9 = 16 + 9
Giờ tính diện tích tổng cộng là h́nh vuông, có cạnh là (x+3) , như thế diện tích là (x+3)2 . Mặt khác, ở vế bên phải của phương tŕnh, ta có 16 + 9 = 25 = 52 . Như vậy, phương tŕnh viết lại thành dạng chính phương
(x + 3)2 = 52
Khai căn thức, ta có ngay, x+ 3 = 5 , và như thế kích thước cung pḥng của vương phi là một h́nh vuông có cạnh là x = 2 sải. Thực ra th́ lời giải c̣n thêm một nghiệm số nữa là x = -8, nhưng lời giải thực sự vẫn là x = 2. Công thức để giải phương tŕnh bậc hai, giờ đây học sinh trung học ai cũng biết.
Phương tŕnh đại số bậc ba có dạng tổng quát là
a x3 + b x2 + c x + d = 0
với x là ẩn số cần phải tính ra, một khi đă biết những hệ số a, b, c và d. Chẳng hạn phương tŕnh đại số bậc ba
x3 - 2 x2 - 5 x + 6 = 0
có những hệ số là a = 1, b = -2, c = -5 và d = 6. Khi đă có những hệ số này mà biết công thức giải toán phương tŕnh bậc ba th́ sẽ t́m ra được ba nghiệm số là x = 1, x = -2 và x = 3 cho phương tŕnh. Công thức để giải phương tŕnh bậc ba tuy hơi phức tạp hơn công thức giải phương tŕnh bậc hai, nhưng cũng được t́m thấy và chỉ cần áp dụng bốn phép tính cộng, trừ, nhân và chia và t́m căn thức là tính được. Trong đại số học, v́ tên của Al-Khowarizme khó nhớ nên công thức giải phương tŕnh bậc hai được gọi là công thức toàn phương, c̣n công thức giải phương tŕnh bậc ba được gọi là công thức Cardan tuy rằng ông không phải là người đầu tiên biết giải phương tŕnh này.
Phương tŕnh đại số bậc bốn có dạng thức tổng quát là
a x4 + b x3 + c x2 + d x + e = 0
mà a, b, c, d và e là những hệ số cho biết và x là ẩn số cần phải tính ra. Một định lư tổng quát được biết là một phương tŕnh bậc n phải có n nghiệm số, những nghiệm số này có thể là nghiệm số thực hay nghiệm số ảo, và cũng có thể có nhiều nghiệm số trùng nhau. Phương tŕnh bâc bốn cũng giải được bằng bốn phép tính cộng, trừ, nhân và chia, và khai căn số bậc hai và bậc ba. Công thức để giải phương tŕnh cũng phức tạp hơn. Trước hết phải dùng những hệ số a, b, … , e để kiến trúc một phương tŕnh bậc ba rồi giải phương tŕnh này để t́m lấy một nghiệm số thực, rồi dùng nghiệm số này cùng với các hệ số cho trước kia để kiến trúc ra hai phương tŕnh bậc hai, mỗi phương tŕnh sẽ cho hai nghiệm số, tổng cộng là bốn nghiệm số cho phương tŕnh bậc bốn nguyên thủy.
Sau khi giải được các phương tŕnh đại số cho tới bậc bốn, các toán gia trải qua gần ba thế kỷ mà không sao giải được phương tŕnh bậc năm
a x5 + b x4 + c x3 + d x2 + e x + f = 0
Họ đă không sao t́m ra được phương pháp chỉ dùng bốn phép tính cơ bản và khai phương để t́m ra 5 nghiệm số cho x, căn cứ vào những hệ số a, b, …, f cho sẵn.
Năm Canh Th́n, Minh Mệnh nguyên niên ở nước ta (1820), th́ ở dưới trời Âu, Abel vừa tṛn 18 tuổi, cái tuổi mà ở thời nay chúng ta vừa học xong trung học. Tự tin ở khả năng của ḿnh, chàng tuổi trẻ biết rằng, chỉ có cách đạt được một thành tích thật siêu việt trong bộ môn toán học và dùng đó làm thẻ bài xin ra mắt các giáo sư lỗi lạc ở các nước Pháp và Đức để được chú ư đến và cấp giấy giới thiệu th́ mới có thể đạt được chức giáo sư hằng mơ ước của ḿnh.
Abel bắt tay vào việc
Vào thời bấy giờ, tuy chưa ai t́m thấy phép giải phương tŕnh đại số bậc năm, nhưng giới toán học đă t́m ra nhiều định lư áp dụng cho phương tŕnh đại số tổng quát bậc n. Người ta vẫn nuôi hy vọng giải được bài toán hóc hiểm này. Vả chăng những phương pháp giải cho tới phương tŕnh bậc bốn đều dựa trên những cách thức biến đổi. Chẳng hạn cho phương tŕnh bậc hai th́ biến đổi thành một chính phương – như phương pháp tính diện tích cung pḥng của bà hoàng phi – rồi tính căn thức là sẽ t́m ra ẩn số. V́ vậy Abel nghĩ rằng nếu chịu khó bỏ ngày giờ ra loay hoay với phương tŕnh bậc năm, sao cũng có lúc t́m ra phương pháp biến đổi và thu gọn lại thành một phương tŕnh giải được bằng căn thức và bốn phép tính cộng, trừ, nhân và chia. Ít lâu sau, chàng tưởng ra là đă t́m thấy phép giải và vị thầy đỡ đầu là Holmboe đă hân hoan gửi bài viết của chàng tới những nhà toán học tên tuổi ở Na Uy và Đan Mạch.
Cũng may cho Abel là phép giải phương tŕnh bậc năm của chàng chưa được công bố ra ngoài v́ các toán gia nhận được bài c̣n viết thư về hỏi thêm ít chi tiết cần làm sáng tỏ. Trong khi ấy Abel t́m ra được rằng lư luận giải của ḿnh có chỗ sơ hở. Cũng v́ chàng thấy rằng con đường đi t́m lời giải cho phương tŕnh đại số bậc năm bị nghẽn lối một cách tuyệt vọng mà Abel t́m ra được chân lư. Nhà toán học trẻ tuổi ở Na Uy đă chứng ḿnh rằng phương tŕnh không có lời giải hữu hạn, nghĩa là không thể tính được trị số của ẩn số x bằng cách dùng bốn phép tính căn bản và phép khai căn như đă làm cho tới phương tŕnh bậc bốn. Lúc đó Abel mới mười chín tuổi. Vào thời nay khi giải những phương tŕnh đại số cao bậc, người ta phải dùng phép tính lập lại, để tính dần dần, và dùng máy điện toán khi những hệ số a, b, … là những con số cho sẵn.
Vào tháng Sáu năm 1822, khi gần tṛn hai mươi tuổi, th́ Abel hoàn tất việc học ở Đại học Kritiania. Ông thầy ở trung học là Holmboe, người đă hết sức giúp đỡ tài chính cho chàng trong những năm qua, đă vận động các giáo chức khác, cùng trong hoàn cảnh thanh bạch, để tài trợ cho Abel được du học, trước hết là tới Pháp, coi như là trung tâm toán học trên thế giới, và tới thăm những đại học có tiếng tăm ở Đức quốc và được gặp giáo sư Gauss, thời đó được coi như vị Bắc Đẩu trong giới toán học. Các thân hữu và giáo sư mến chuộng tài năng của chàng đă đề nghị lên chính phủ để cấp cho chàng một ngân khoản để thăm những nước chính ở Âu châu. Trong khi đó th́ Abel cũng đă tự bỏ tiền ra để in một tài liệu quan trọng, trong đó có bài chứng minh rằng phương tŕnh đại số bậc năm không thể giải được bằng phép khai căn và bốn phép tính căn bản. Ai cũng nghĩ rằng chuyến thăm viếng này sẽ đưa lại sự chú ư của các nước tân tiến, đặc biệt là Pháp và Đức, cho nền giáo dục ở Na Uy, qua tài năng của Abel.
Tiếc thay tất cả những vận động ấy chỉ đưa đến kết quả là chàng được tài trợ để tiếp tục theo học ở Kristiania, trau dồi thêm về ngoại ngữ Pháp và Đức. Chàng sinh viên, hay nói cho đúng hơn, toán gia có tài năng, đă nhận lănh không chút phàn nàn học bổng ấy để có th́ giờ nghiên cứu thêm về toán học. Cùng một lúc Abel cố gắng vật lộn với văn phạm Đức và Pháp để chờ ngày có phương tiện xuất ngoại. Khoảng thời gian ở lại học thêm, Abel hứa hôn với một thiếu nữ tên là Crelly Kemp và được người bạn yêu qúy, chàng cũng quên được những cực nhọc khi phải dạy học thêm để kiếm tiền nuôi các em.
Rồi ngày mong đợi của chàng cũng tới khi một sắc lệnh của quốc vương kư ngày 27 tháng Tám năm 1825 ban cho Abel một ngân khoản đủ để đi tu nghiệp một năm ở Pháp và Đức. Chàng mất chừng một tháng để thu xếp ổn định tài chính cho mẹ và các em trước khi lên đường.Nhưng cái mộng được gặp đại toán gia người Đức là Friedrich Carl Gauss (1777-1855), Abel đă gạch bỏ từ lâu. Trước đó hơn một năm, chàng gửi đến giáo sư Gauss ấn tŕnh của ḿnh về chứng minh rằng phương tŕnh bậc năm không có phép giải. Ta nên nhớ lại là trải qua ba trăm năm không ai t́m ra phép giải, và cũng v́ vậy toán gia Gauss khi nhận được tài liệu này, nh́n thoáng qua ông tưởng như là lại có người khoe phương pháp mới nên đă quẳng ngay vào sọt rác và nói rằng: ”Lại thêm một bài lẩm cẩm nữa”.
Nhắc lại chuyện này, có nhiều người nghĩ rằng nếu Gauss b́nh tâm một chút, đọc bài viết sẽ nhận ra ngay rằng đây không phải là bài giải phương tŕnh, là điều tất nhiên không ai làm được, mà là bài đầu tiên chứng minh rằng phương tŕnh không có phép giải hữu hạn. Vị bắc đẩu trong giới toán học sẽ t́m thấy trong Abel một thiên tài rồi sẽ sáng chói, và một lời giới thiêu của Gauss sẽ đỡ được cho Abel biết bao nhiêu cơ cực, và biết đâu lại cho chàng thêm được chút tuổi trời.
Sau khi nhận học bổng, Abel lên đường vào tháng Chín năm 1825 và tới thăm các toán gia tên tuổi của Na Uy và Đan Mạch. Trước kia chàng mong mỏi được yết kiến thần tượng của ḿnh là toán gia Gauss, nhưng nay th́ h́nh ảnh đẹp ấy không c̣n nữa, chàng đi thẳng tới Berlin và ở đây anh đă gặp được duyên may đưa nhà toán học trẻ tuổi lên bước đường danh vọng. Ở đây chàng gặp một kỹ sư kiều lộ có năng khiếu toán học là ông August Leopold Crelle (1780-1856). Ông kỹ sư này, nhờ công tŕnh kiến thiết đường xe hoả đầu tiên cho Đức quốc mà được hoạnh tài, và ông đă dùng số vốn đó để ra môt tờ báo gọi là Nguyệt San Toán Học Thuần Lư và Áp Dụng (Journal fur die reine und angewandte Mathematik) số đầu tiên được phát hành năm 1826. Thực sự, Crelle chỉ là một người yêu toán học hơn là môt toán gia, nhưng trải qua hơn một thế kỷ, dù hiện nay có hàng trăm tờ báo trên thế giới chuyên ngành toán học dưới đủ mọi bộ môn và tŕnh độ, giới toán học vẫn ghi nhận sự đóng góp căn bản của ông đă đi tiên phong để ra một tờ báo phục vụ môn toán học. Tờ báo của Crelle đă làm rạng rỡ tên tuổi của Abel v́ ba năm đầu tiên, báo đă đăng hai mươi hai bài khảo cứu của chàng. Người đương thời, ai cũng phải công nhận là ngoài năng khiếu kinh doanh, Crellle đă có tài t́m ra những chân tài toán học. Người ta kể lại sự gặp gỡ giữa hai người như sau.
Khi Abel tới Berlin vào năm 1825, th́ lúc đó Crelle c̣n là một công chức có nhiệm vụ khảo hạch thí sinh thi tuyển vào trường Công Nghệ, dù rằng ông đang chuẩn bị để sẽ ra báo. Một hôm vào buổi sáng đẹp trời, ông thấy môt thanh niên, trông c̣n rất trẻ và tuấn tú, có vẻ rụt rè khi bước vào pḥng giấy của ḿnh. Ông tưởng đó là một thí sinh muốn nhập học trường Công Nghệ nên bắt đầu giảng giải rằng anh ta sẽ phải trải qua nhiều kỳ thi riêng biệt chứ không phải chỉ với ông mà thôi. Chàng tuổi trẻ trả lời ấp úng bằng môt thứ tiếng Đức bập bẹ là: “không có thi, chỉ nói toán thôi!”. Crelle biết ngay chàng thanh niên là người ngoại quốc không thông thạo tiếng Đức nên xoay ra tiếng Pháp và Abel bớt lúng túng nhưng cũng phải vất vả lắm mới tŕnh bày nổi ư kiến của ḿnh. Thoạt đầu Crelle hỏi Abel là đă theo đuổi toán học đến tŕnh độ nào th́ được chàng trả lời môt cách rất khôn ngoan là đă đọc một bài viết của Crelle vào năm 1823 về phép tính giai thừa và lấy làm thích thú. Nhưng sau đấy v́ say xưa nói về toán học, Abel đă thiếu tế nhị và thẳng thắn phê b́nh là ở trong bài có nhiều đoạn viết sai. Cái tài xuất chúng của Crelle không phải trong phạm vi toán học, mà ở chỗ biết ḿnh và biết người. Ông đă không chạm tự ái để nổi nóng với một kẻ hậu sinh, nhưng đă ôn tồn hỏi thêm về những điều Abel đă học hỏi được và t́m ṭi thêm ra. Hai người đă nói chuyện rất lâu và sau này Crelle đă kể lại rằng nhiều vấn đề Abel nói ra đă vượt tầm hiểu biết của ông. Crellle đă đi đến kết luận là trong tương lai Abel sẽ là một toán gia siêu việt, và khi báo của ông ra đời th́ chàng sẽ là một trong những cộng sự viên tiên khởi. Môt trong những bản thảo Abel đă đưa ra là bài chứng minh rằng phương tŕnh đại số bậc năm không có lời giải hữu hạn- tức là phải tính lập lại nhiều lần mới t́m ra trị số của ẩn số. Mới đầu Crelle cũng không tin, và lúc cầm đọc bản thảo ông cũng không hiểu hết, nhưng vẫn đưa Abel tới những nơi hội họp và giới thiệu chàng như là một thiên tài toán học. Đôi khi ông đưa cùng theo một toán gia trẻ tuổi khác ông đă khám phá ra là nhà toán h́nh học Jacob Steiner người Thụy Sĩ. Chàng tuổi trẻ này là người đầu tiên chứng minh không để sơ hở một tính chất h́nh học người ta thường biết theo trực giác là một h́nh phẳng có chu vi cho sẵn mà được diện tích lớn nhất th́ h́nh đó phải là h́nh tṛn. Tính chất này đă được biết từ thời thượng cổ nhưng phải đợi đến thời của Steiner (1796-1863) dùng tính chất của h́nh lồi và pháp đối xứng mới chứng minh được một cách thấu triệt.
Những giao tế thăm viếng ở Berlin cũng đă một phần nào ảnh hưởng đến công tŕnh khảo cứu của Abel. Chàng đă lui về tỉnh Freiburg một thời gian và ở đây Abel đă t́m ra được một định lư về một họ phương tŕnh siêu việt và để lại cho hậu thế “Định Lư Abel”. Gần hai trăm năm sau, ở vào thời đại nguyên tử tối tân, và đă sang thiên niên kỷ hai ngàn, chương sách về định lư Abel và những áp dụng vẫn là một phần quan trọng trong chương tŕnh Toán bậc cao học trong các đại học ở khắp năm châu.
Theo chương tŕnh thăm viếng đă được đề ra với học bổng của chàng, Abel tới Paris và xin tới thăm những toán gia vĩ đại thời ấy như Legendre, Cauchy, Poisson, Fourier … Chàng thấy ngay là người Pháp tuy lịch sự nhưng rất lạnh lùng và kiểu cách. Tới xin ra mắt một vị nào, chưa kịp tŕnh bầy ư kiến của ḿnh, chàng đă thấy chủ nhân thuyết giảng về những công tŕnh vĩ đại của riêng ḿnh. Nói tóm lại, sau bốn tháng trời ở Paris, Abel đă không được ai chiếu cố tận t́nh, không được mời thuyết tŕnh một lần dầu rằng chàng cũng có một chút tên tuổi qua những bài đăng trên báo của Crelle. Chàng viết thư cho thầy học cũ là Holmboe ở Na Uy và nói là sẽ từ giă Paris để đi về miền Nam ấm cúng hơn và rồi sẽ qua Thụy Sĩ trước khi trở về quê hương.
Trước khi rời thủ đô nước Pháp, Abel đưa công tŕnh vĩ đại của ḿnh về hàm số siêu việt cho nhà toán học Augustin-Louis Cauchy (1789-1857), lúc đó 39 tuổi, và đang trong thời kỳ sáng tác phong phú. Mặc dầu ông Hàn lâm này có nhiệm vụ cùng với nhà toán học Adrien-Marie Legendre (1752-1833), đă 74 tuổi, duyệt xét bài viết của Abel, ông lại để cho một vị khác kém tên tuổi là Hachette ra tŕnh bày cho có lệ ở buổi họp ngày 10 tháng Mười, năm 1826 của Hàn Lâm Viện Khoa Học. Sau đó Cauchy mang bài về nhà rồi để lạc ở đâu mất. C̣n Legendre th́ mấy năm sau viết trả lời thư khiếu nại của nhà toán học Jacobi và kể rằng bài viết bằng mực lờ mờ rất khó đọc nên đă nhắn với tác giả viết lại bản mới. Lúc đó là những tháng đầu năm 1829, và Abel đă trở về Na Uy, sức khoẻ tàn tạ. Carl Gustav Jacob Jacobi (1804-1851), lúc đó là một nhà toán học trẻ người Đức và là một ngôi sao sáng đang lên; ông đă viết một bức thư đề ngày 14 tháng Ba năm 1829 đả kích kịch liệt Hàn Lâm Viện Khoa Học Pháp đă lơ là với một tác phẩm vĩ đại gửi đến cho họ. V́ thế mà có những lới phân trần kể trên của ông Hàn Legendre. Toà Lănh sự Na Uy cũng đặt vấn đề với chính phủ Pháp và Cauchy cũng phải lục đám hồ sơ cũ để t́m ra bản thảo của Abel. Để đền bù lại, Hàn Lâm Viện Khoa Học Pháp tặng Giải Ưu Hạng về Toán Học năm 1830 chung cho Abel và Jacobi.
Trước khi có những cuộc chỉ trích, tranh luận và phân trần ấy th́ Abel đă trở về Na Uy từ tháng Năm năm 1827, tiền nong đă cạn, lại thêm bệnh phổi trầm trọng, tới thời kỳ cuối cùng. Chàng vẫn hy vọng được chức giáo sư vừa trống ở Đại Học Kristiania. Một điều đáng tiếc là ở đại học, Hội Đồng Quản Trị bắt buộc ông Holmboe phải nhận ghế giáo sư toán này mặc dầu ông này hết sức đề bạt cho Abel là người xứng đáng hơn. Sau cùng Holmboe miễn cưỡng nhận v́ ông Viện trưởng dọa là nếu không sẽ mời một giáo sư ngoại quốc tới để nhận ghế giáo sư đó.
Từ đầu năm 1929, Abel biết ḿnh không c̣n sống được bao lâu nữa. Chàng ở tỉnh Froland, trú ngụ tại gia đ́nh một người Anh Cát Lợi mà cô Crelly Kemp đang là quản gia. Những ngày cuối của cuộc đời, chàng đă nghĩ đến tương lai của người vợ chưa cưới này và đă viết cho người bạn thân tên là Kielhau rằng: “Tuy cô không đẹp, có bộ tóc đỏ và mặt có tàn nhang, nhưng sẽ là người vợ tuyệt vời”. Chàng ước nguyện là hai người sẽ lấy nhau tuy rằng cô bạn gái đă nhất quyết là săn sóc cho chàng cho đến phút cuối cùng. Sáng ngày 6 tháng Tư năm 1829, Abel vĩnh biệt cuộc đời, hưởng dương hai mươi sáu năm tám tháng.
Hai ngày sau khi chàng mất th́ ông kỹ sư và chủ báo Crelle, lúc đó chưa biết tin, đă viết thư báo tin là đă vận động thành công cho Abel được bổ nhiệm là giáo sư toán học ở Đại học Berlin. C̣n bản thảo công tŕnh đặc sắc nhất của chàng th́ tới năm 1841 mới được in trong tập san định kỳ “Mémoires présentés par divers savants à l’Académie royale des sciences de l’Institut de France” số 7, trang 176-264.